[수학] 삼각함수(3) 변의 명칭과 삼각비

수학

[수학] 삼각함수(3) 변의 명칭과 삼각비

Artiper

|2024. 8. 26. 15:06

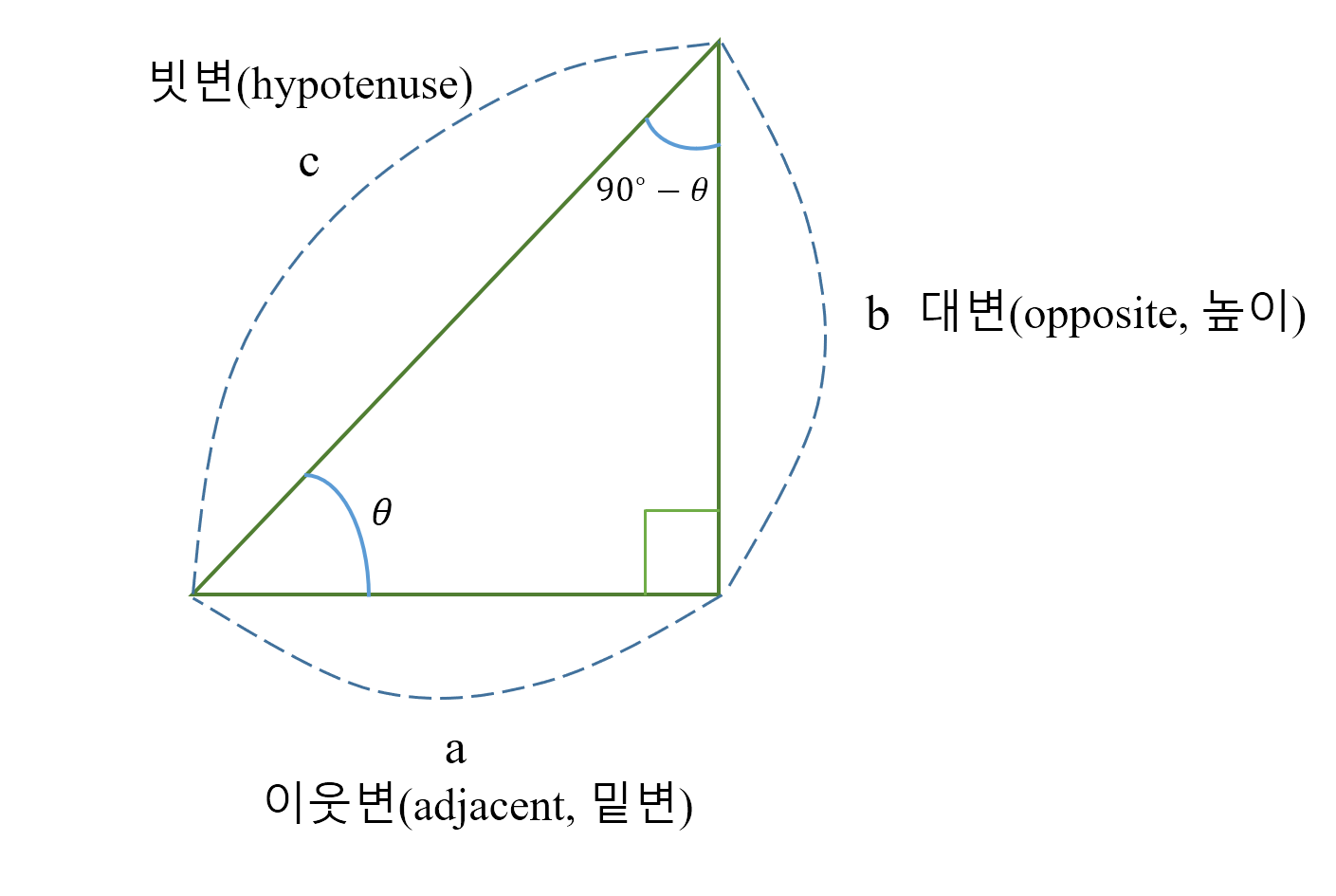
변의 명칭

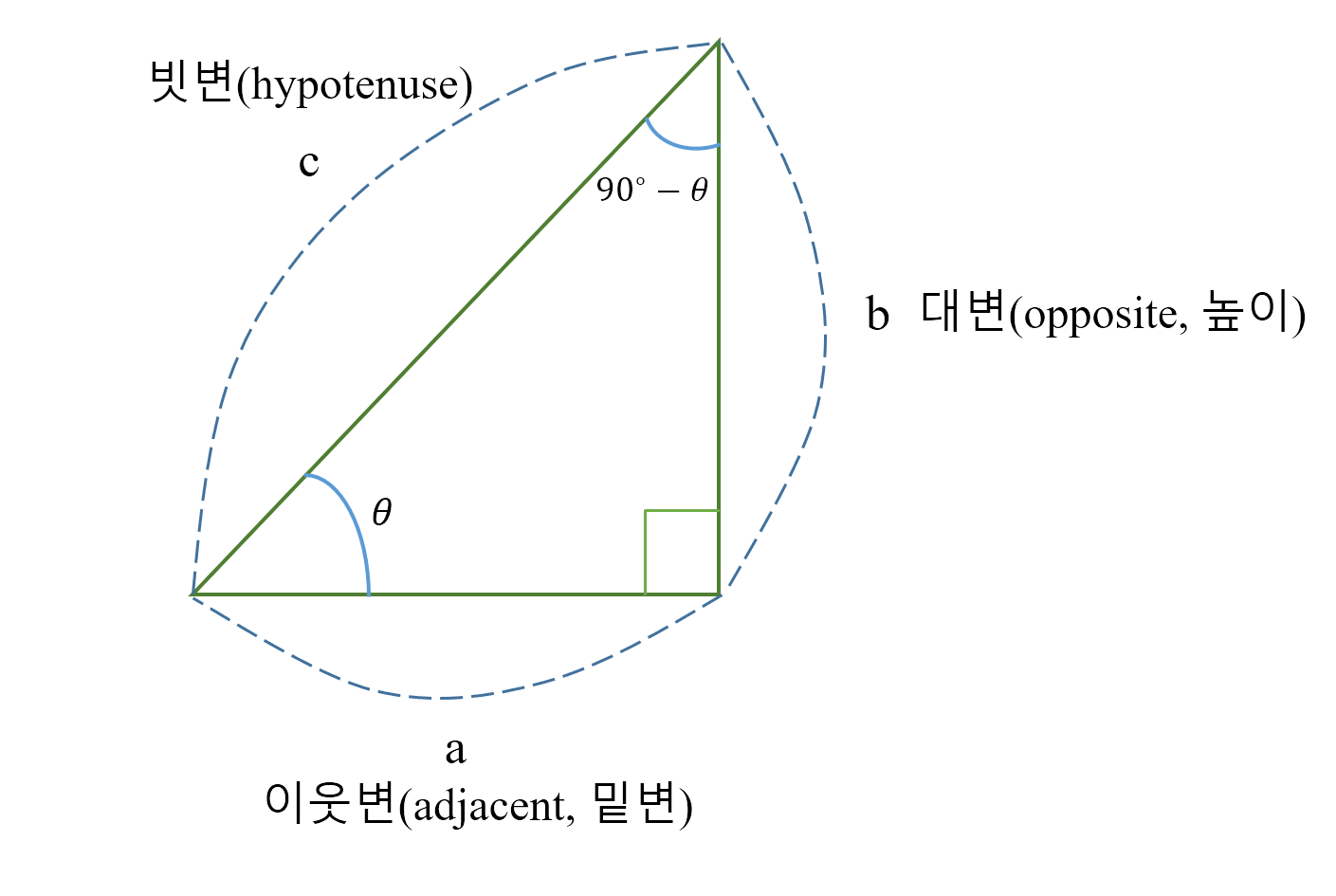
삼각비 계산을 헷갈리지 않도록 하려면 변의 정의가 중요하다. 영어 명칭이 이해하기 편하여 같이 작성하였다.

빗변(hypotenuse)은 직각의 대변에 위치한다.
이웃변(adjacent)은 각 $\theta$와 인접하여 이웃변이라 하며, 밑변이라고도 한다.
대변(opposite)은 각 $\theta$와 마주보고 있어 대변이라 하며, 높이라고도 한다.

평균적으로 이웃변과 대변은 밑변과 높이로 불려서 많이 사용된다.

삼각비(Trigonometric Ratio)

삼각비란 직각삼각형의 성질을 이용한 내용이다. 직각삼각형에서 직각을 제외한 각인 $\theta$에 대해 직각삼각형의 세 변의 길이가 이루는 비율이 일정함을 발견하였다. 그래서 각 $\theta$가 유지만 된다면, 삼각형의 크기(변의 길이)가 달라지더라도 변들의 비율은 일정하다는 것이다. 이 삼각비 덕분에 각을 통해 길이를 잴 수 있게 되었다.

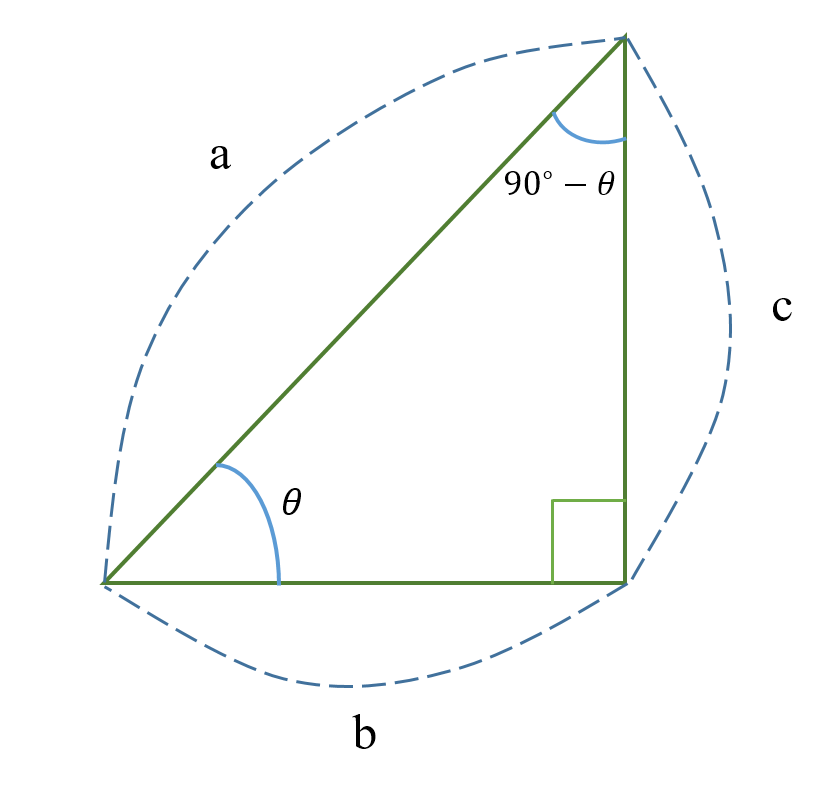
$\theta$만 유지되면 삼각형의 크기가 달라지더라도 즉, 닮음을 유지할 수 있는 이유는 단순한데 삼각형에서 두 각의 각도가 같다는 의미는 세 각의 각도도 똑같다는 의미이기 때문이다. 그래서 직각을 제외한 $\theta$의 각도만 동일하다면 직각삼각형의 크기가 달라져도 닮음꼴을 유지할 수 있다. 즉, 삼각비란 특정 각도에서 변들 사이의 비율을 나타낸 것이다.

삼각비의 종류

위 내용에서 삼각비란 직각삼각형의 특정 각도에서 변들 사이의 비율을 나타낸 것이라고 설명하였는데, 삼각형에서 변은 3개이니 비율 계산 방법이 하나만 존재하진 않을 것이다. 우리가 알아볼 것은 총 3가지의 삼각비인 sin, cos, tan이다. sin, cos, tan는 각각 다음과 같이 정의된다:

$sin = \frac{높이}{빗변}$
$cos = \frac{밑변}{빗변}$
$tan = \frac{높이}{밑변}$

사실 이를 외울 때 밑변과 높이는 나한테 있어 헷갈리는 감이 있어, 변의 이름을 영어로 하는 것이 더 잘외워졌는데, soh-cah-toa 방식으로 외우는 것이 좋았다.

$sin = \frac{opp}{hyp}$
$cos = \frac{adj}{hyp}$
$tan = \frac{opp}{adj}$

또한 이를 일반적으로 나타낼 때는 각에 대해 삼각비를 표기하는데, 각 $\theta$에 대해 sin, cos, tan값을 표기하면 다음과 같다.

$sin\theta = \frac{높이}{빗변}$
$cos\theta = \frac{밑변}{빗변}$
$tan\theta = \frac{높이}{밑변}$

왜 삼각비의 명칭이 sin, cos, tan이 되었는지는 해당 유튜브 영상에서 확인할 수 있다.

sin, cos, tan 비율값 구하기 예제

문제 원본 링크

이는 칸 아카데미에서 가져온 문제이며, sin, cos, tan를 어떻게 설정해야 하는지를 잘 학습할 수 있다.

빗변, 높이, 밑변의 위치를 헷갈리지 않도록 하자.

문제 1

정답

$ cos(F) = \frac{5}{13}$
$ sin(F) = \frac{12}{13}$
$ tan(F) = \frac{12}{5}$

문제 2

문제 원본 링크

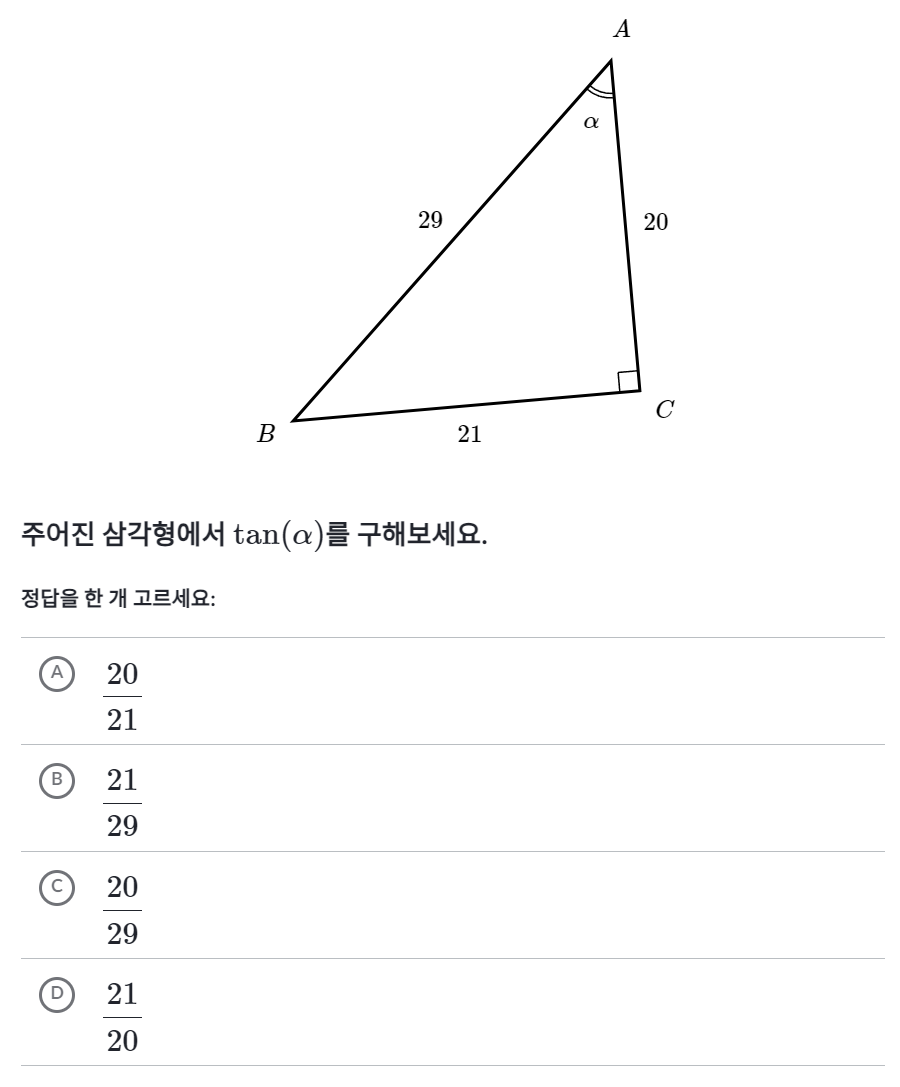
정답

D - $\frac{21}{20}$

삼각비는 각도마다 값이 다른가?

삼각비는 직각을 제외한 $\theta$의 각도만 동일하다면 직각삼각형의 크기가 달라져도 닮음을 유지할 수 있다고 하였지만, 이 의미는 각도 $\theta$가 조금이라도 달라진다면, 이에 따른 sin, cos, tan 비율이 달라진다는 의미도 된다.

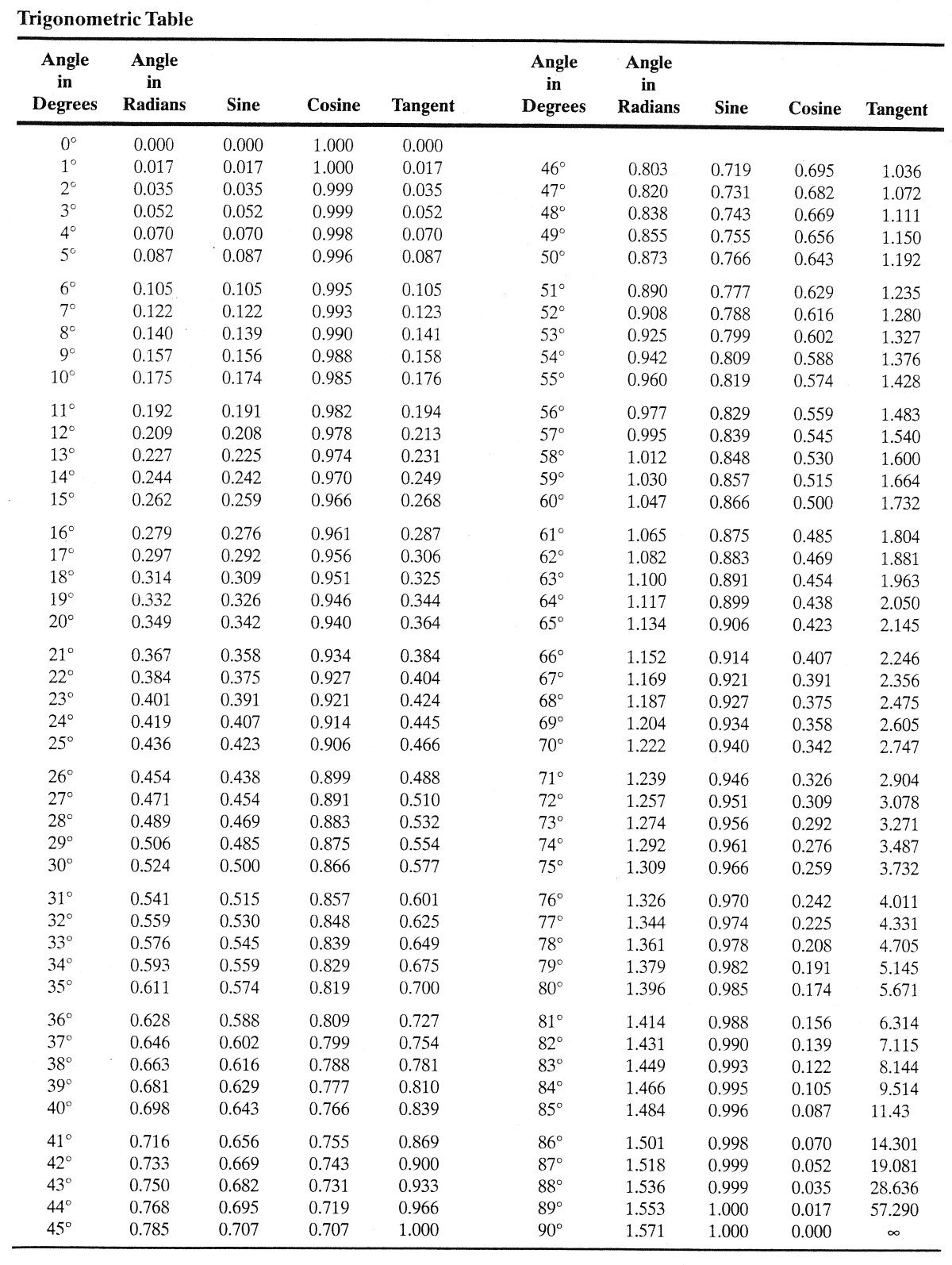
https://academics.uccs.edu/rtirado/Trigonometric%20Table.pdf

그래서 이 표와 같이 $1^\circ$마다 sin, cos, tan의 비율을 구하여 표로 정리해놓은 자료들이 존재한다. 그리고 여기서 $0^\circ, 30^\circ, 45^\circ, 90^\circ$은 삼각비의 특수각이라 불리는데, 그 이유는 값이 딱 맞아 떨어지기 때문이다.

삼각비의 특수각

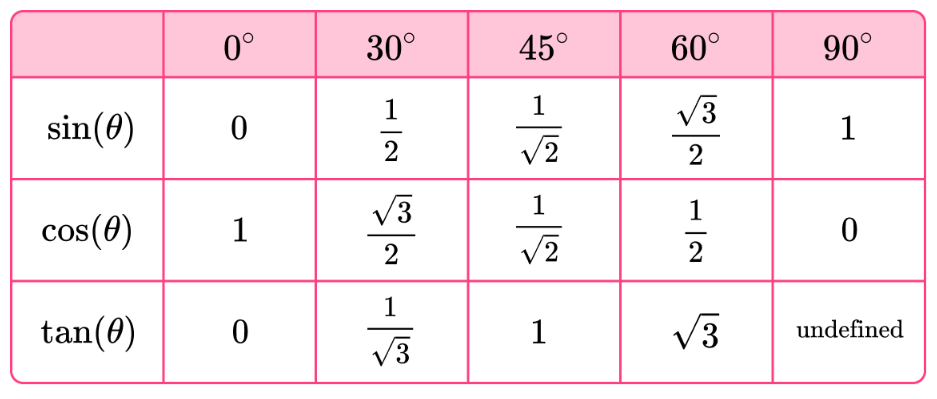
https://thirdspacelearning.com/gcse-maths/geometry-and-measure/trigonometry-table/

이처럼 삼각비의 특수각을 확인할 수 있다. 즉, $sin^\circ 30$을 예로 들자면 해당 비의 값은 $\frac{1}{2}$라는 의미인데, 이를 어떻게 활용하는지 다음 예제 문제에서 확인하자.

sin, cos, tan을 문제에 적용

문제

한 사람이 지면과 평행하게 30m 떨어진 위치에서 건물의 꼭대기를 바라보고 있다. 이때 사람의 시선과 지면 사이의 각도가 $45^ \circ$이다. 건물의 높이를 구하시오. (단, 사람의 눈높이는 무시한다.)

풀이

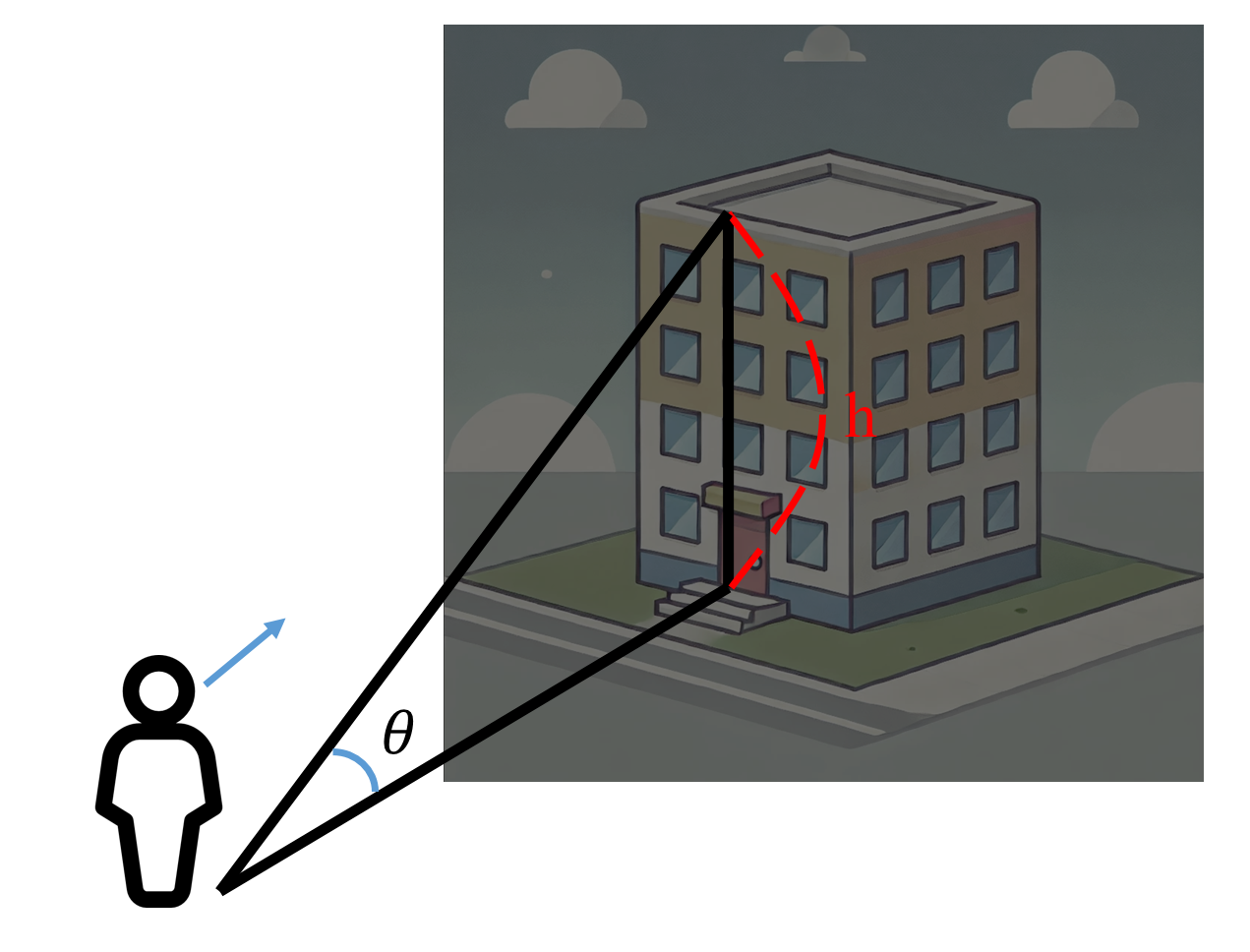
이 문제를 풀기 위해 탄젠트를 이용한다. 탄젠트는 $\frac{높이}{밑변}$인데, 여기서 밑변은 사람과의 거리로 볼 수 있다. 그래서 $tan(\theta) = \frac{h}{30}$이며, $\theta=45^\circ$이므로 $tan(45^\circ) = \frac{h}{30}$이다.으로 둘 수 있다. 그리고 특수각을 참조하면 $\tan(45^\circ)=1$이므로, $1=\frac{h}{30}$이다. 즉, $h=30m$이다.

물론 사인과 코사인도 사용 가능하다. 탄젠트가 가장 구하기 쉬웠으니 사용한 것뿐이다. 사인과 코사인을 이용한다면, 코사인을 통해 빗변을 구한 뒤 사인을 통해 높이를 구하면 된다.

삼각비의 적용범위

삼각비는 직각삼각형을 기준으로 정의된 내용이다. 직각삼각형에서 직각이 아닌 다른 두 개의 각 중 하나 $\theta$로 두고, $\theta$에 대해 정의한 것이다. 여기서 $\theta$는 무조건 예각일 수 밖에 없는데, 당연히 삼각형의 전체각도에서 직각을 제외하면 남은 두 각의 합은 최대 90$^\circ$만 남는데, 여기서 $\theta$는 최대 89.9$^\circ$는 되더라도 90$^\circ$는 되지 못한다. 그래서 $\theta$는 90$^\circ$보단 작고, 0$^\circ$보단 클 수 밖에 없기에 예각일 수 밖에없다. 이 한계점을 극복하기 위해 삼각함수를 사용할 수 있다.

참고자료

'수학' 카테고리의 다른 글

[수학] Manhattan distance (맨해튼 거리) (1)	2024.09.21
[수학] 삼각함수(4) 삼각함수 (0)	2024.08.26
[수학] 삼각함수(2) 호도법 (0)	2024.08.22
[수학] 삼각함수(1) 원의 개념 (0)	2024.08.20
L1-Norm, L2-Norm (0)	2024.04.21