L1-Norm, L2-Norm

Norm

기하학적 해석을 위해 존재한다. 벡터 사이의 길이와 거리를 재는 방법이며, 벡터 공간 V에서 norm은 함수이다.

Norm 함수는 각 벡터 $x$의 그 자체의 길이 $\lVert x \rVert \in \mathbb{R}$를 할당한다. 모든 $\lambda \in \mathbb{R}$, $\lambda$는 실수집합 내이고, $x, y \in V$, $x,y$는 vector space안의 원소이므로 다음을 따른다:

 

- 동차 함수

- 삼각 부등식

- 양의 정부호

-- (if and only if, 필요 충분 조건, $\iff$)

 

 

 

Trainalge ineaulity (삼각 부등식)

MML 책의 figure 3.2

 

삼각 부등식이란, 삼각형에서 임의의 두 변의 합이 나머지 한 변보다 크거나 같아야 을 의미한다. 

위키백과 삼각 부등식 설명 사진

 

위키백과 이미지에 따르면 x와 y의 합이 z에 가까워질수록 하나의 선분으로 합쳐지는 결과를 확인할 수 있다.

 

 

 

 

Positive definite

양수가 작동하는 방식이 그대로 적용된다는 의미. 부호의 변화는 시키지 않고, 크기의 변화만 시킨다.

 

 

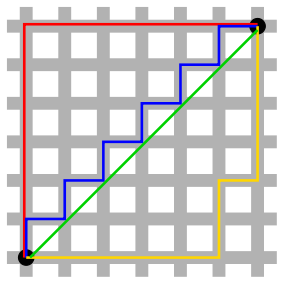
L1-Norm (Manhattan distance)

맨하탄 거리로 각 원소의 절대값의 전체 합이다.

 

 

L2-Norm (Euclidean distance)

L2-Norm은 원점으로부터 거리를 구하기에, 피타고라스를 통해 구해진다. 이에 대한 수식은 추가적으로 작성할 예정. Frobenius Norm이라고도 불린다.

 

 

 

 

참고 자료

- https://ko.wikipedia.org/wiki/%EC%82%BC%EA%B0%81_%EB%B6%80%EB%93%B1%EC%8B%9D

- https://eehoeskrap.tistory.com/227