원본 자료입니다. 원문을 읽으며 제가 이해한 내용을 추가적으로 작성하였습니다.
Red Blob Games: Hexagonal Grids
Amit's guide to math, algorithms, and code for hexagonal grids
www.redblobgames.com
Hexagonal Grids
해당 가이드는 Hexagonal grid를 만드는 다양한 방법, 다양한 접근 방식의 관례, 일반적인 공식과 알고리즘에 대해 다룬다.
Geometry
육각형은 6개의 변을 가진 다각형이다. 정육각형의 모든 변은 같은 길이를 가진다. Hexagonal grid의 작업은 정육각형을 사용한다고 가정한다.

정육각형의 크기는 변(edge)에 닿는 안쪽원, 꼭짓점에 닿는 바깥족 원으로 설명할 수 있다. 해당 페이지에서는 바깥원의 반지름을 크기로 사용한다. 즉, 꼭짓점에서 시작하여 꼭짓점까지의 거리를 재는 방식(circumradius). Flat-top에서 좀 더 보기 쉬운 크기 측정 방식일 것이다. inner circle 방식은 inradius로, 변의 중심부터 변의 중심까지의 거리를 재는 방식이다.


Spacing
다음으로는 여러개의 육각형을 합치려고 한다.
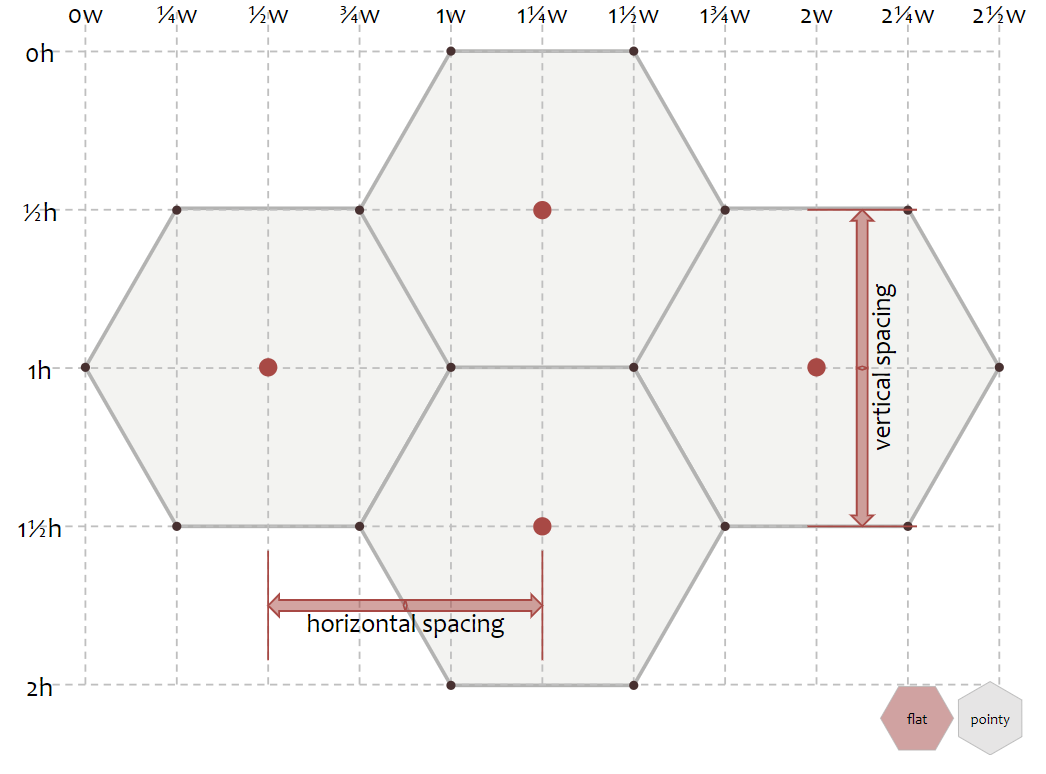
flat top 방향에서 horizontal distance는 인접 육각형의 중앙 사이의 거리는 다음과 같다; $horiz = \frac{3}{4} * width$.
- 좌표계에서 생각해보면, 바깥원의 지름 길이는 총 4칸이며, 다음 육각형과의 거리는 총 3칸이다. 즉 $\frac{3}{4}$ 만큼의 비율을 육각형의 가장 긴 가로길이에 곱하면 horizontal distance를 구할 수 있다.
- 반지름은 $size = 3$이라 가정한다.
- $width = 6 = size * 2$
- $horiz = 4.5 = \frac{3}{4} * width$
- $horiz = 4.5 = \frac{3}{2} * size$
- $horiz = 4.5 = \frac{3}{2} * size$는 반지름에서 3칸만큼의 길이의 비율(1.5)을 곱해주어 horizontal distance를 구하는 방법이다.
- 위 그림을 참고하였을 때, size의 크기 자체는 2칸이다. 그러나 수평 거리가 멀어져있는 거리는 3칸이므로 size의 칸수(비율)을 분모에 두고 이동해야하는 거리를 3칸으로 둔 뒤, 정육각형의 실제 한 변의 길이인 size를 곱해주는 방식이다.
- 좀 더 자세히 설명하자면 수평 거리는 $\frac{size}{2} + size$ 이다. 이는 $\frac{size}{2} + \frac{2size}{2}$로 볼 수 있으며, $\frac{3size}{2}$이 되어 $\frac{3}{2} * size$가 될 수 있다.
flat top 방향에서 인접한 육각형 중심의 세로 방향의 거리는 $vert = height = \sqrt{3} * size$이다. 해당 값을 계산하는 방식은 다음과 같다.

- 육각형은 총 6개의 정삼각형으로 나눌 수 있다.
- 여기서 h의 값을 구하려 할 때, 피타고라스 정리를 사용할 수 있다.
- $h^2 + \left( {\frac{r}{2}} \right) ^2 = r^2$
- $h^2 = r^2 - \left( {\frac{r}{2}} \right) ^2$
- $h^2 = \frac{4r^2}{4} - \frac{r^2}{4}$
- $h^2 = \frac{3r^2}{4}$
- $h = \frac{\sqrt{3}r}{2}$
- 여기까지가 h의 값이다. 육각형 하나의 높이만큼의 vertical spacing을 구하려면 여기서 $2$를 곱하면 된다.
- $vert = height = \sqrt{3} * size$
- 여기서 size는 $r$인 반지름을 의미한다.
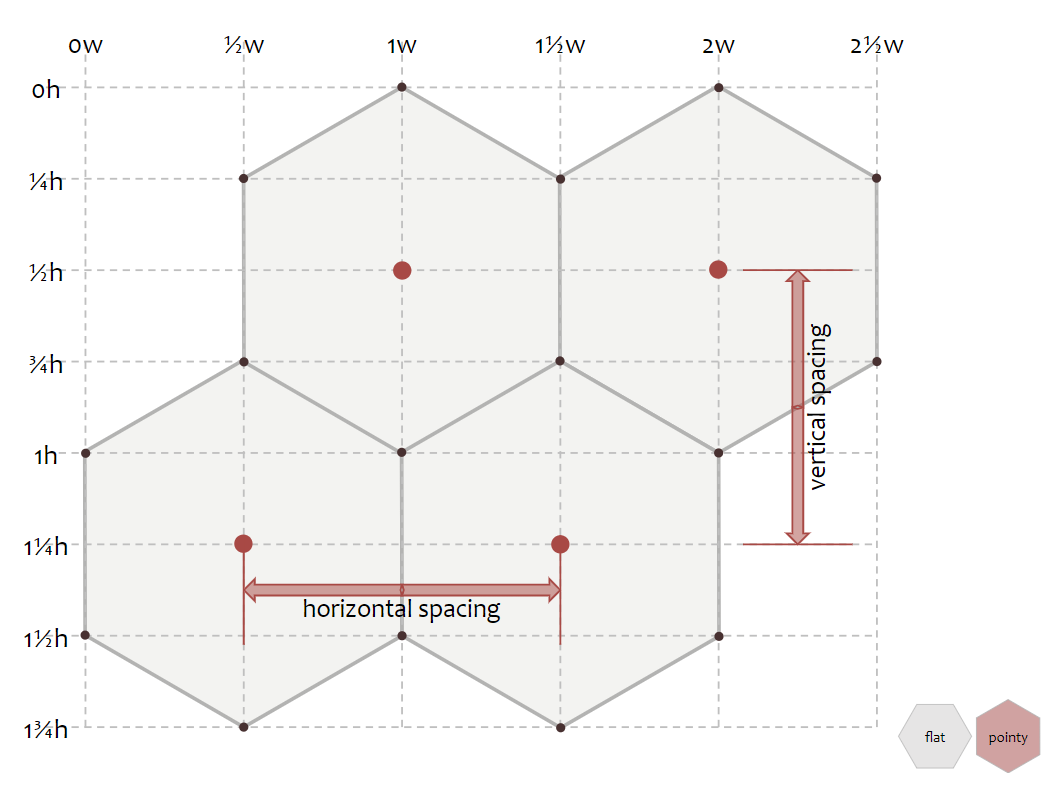
pointy top 방향에서 인접 육각형의 중심에서 수평 거리는 $horiz = width = \sqrt{3} * size$이며, 수직 거리는 $vert = \frac{3}{4} * height = \frac{3}{2} * size$이다.
일부 게임에서는 육각형에 정확히 규칙적인 다각형과 일치하지 않는 픽셀 아트를 사용하므로 이러한 공식을 약간 조정해야 한다. 자세한 내용은 구현 가이드를 참조.
Angles
정육각형에서 내각은 120도이며, 6개의 빗변을 가지고 있다. 6개의 빗변은 내부 각도가 60도인 정삼각형을 각각 가지고있다. 모서리(corner)마다 size 단위로 육각형의 중심에서 떨어져있으며, 코드는 다음과 같다:
function pointy_hex_corner(center, size, i):
var angle_deg = 60 * i - 30°
var angle_rad = PI / 180 * angle_deg
return Point(center.x + size * cos(angle_rad),
center.y + size * sin(angle_rad))
육각형을 채우려면 다각형 꼭짓점을 hex_corner(..., 0)에서 hex_corner(..., 5)까지 모은다. 육각형의 윤곽을 그리려면 해당 정점을 사용한 다음 다시 hex_corner(..., 0)까지 돌아가는 선을 그린다.
두 방향의 차이는 회전으로 인해 각도가 달라지는데, flat top 각도는 0°, 60°, 120°, 180°, 240°, 300°이고 pointy top 각도는 30°, 90°, 150°, 210°, 270°, 330°이다. 이 페이지의 다이어그램은 Y축이 아래를 가리키는 경우(각도는 시계 방향으로 증가)를 사용한다. 만약 y축이 위를 향하도록(각도가 반시계방향으로 증가) 하려면, 조금의 조정이 필요할 수 있다.
해당 코드는 슈도코드인데, 이를 유니티에서 한 번 사용해볼 예정이다.
Coordinate Systems
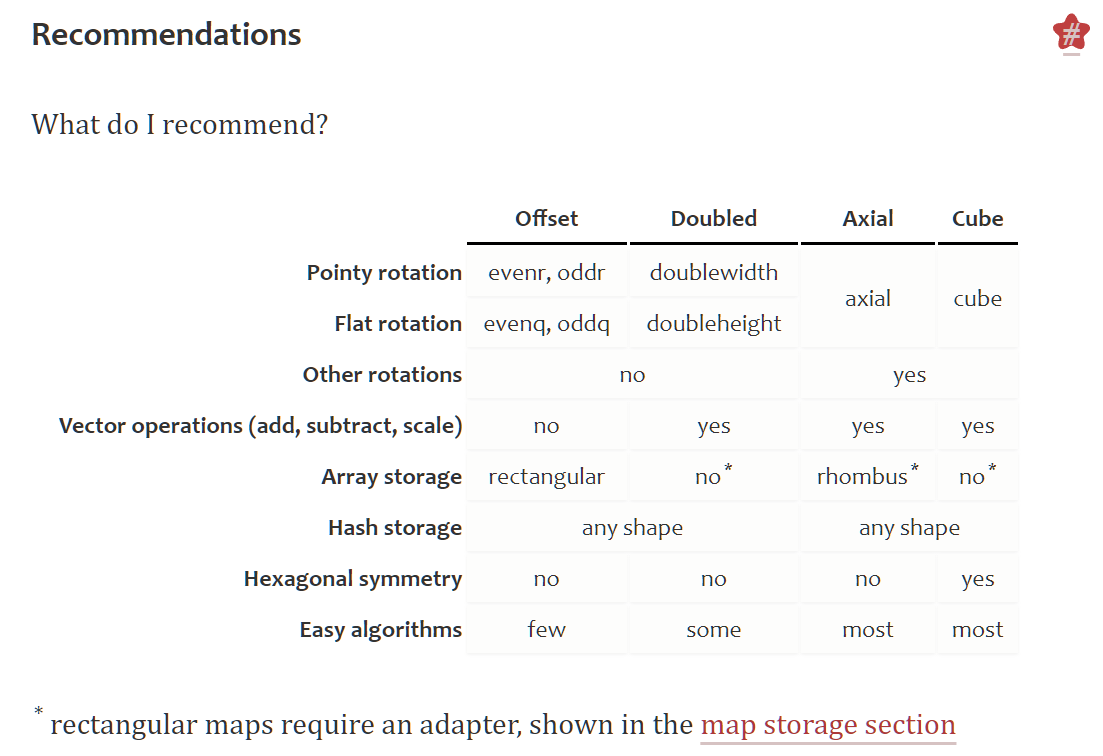
정사각형 Grid와 달리 육각형은 여러 방식이 존재한다. 글 작성자는 알고리즘에는 Cube coordinate를 선호하고, 저장에는 axial 또는 doubled coordinate를 선호한다고 한다.
Offset coordinates
가장 일반적으로 사용되는 방식은 서로 다른 열과 행을 offset 하는 것이다. 열은 $q$, 행은 $r$으로 표기한다. 홀수 또는 짝수 열/행의 오프셋을 지정할 수 있다. 그래서 수평 및 수직 육각형에는 각각 두 가지 변형이 있다.




보통 Axial, Cube 좌표를 권장하지만 offset 좌표를 고수하고 싶은 경우 doubled variant 좌표를 고려해보라고 한다.
Cube coordinates
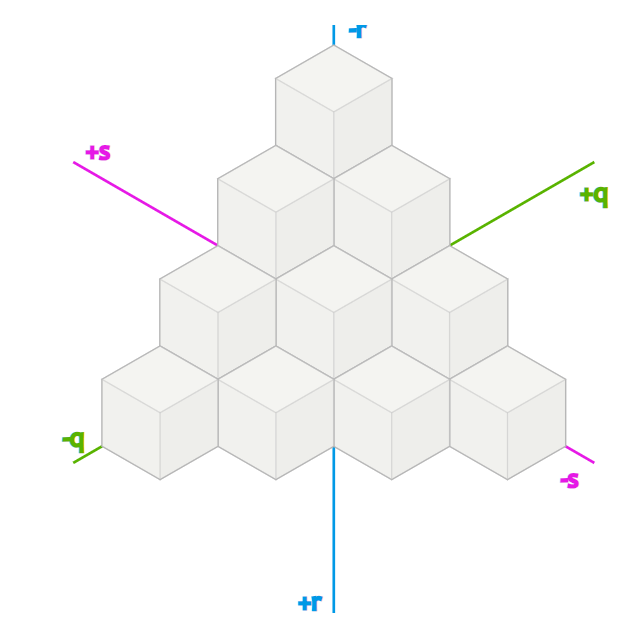
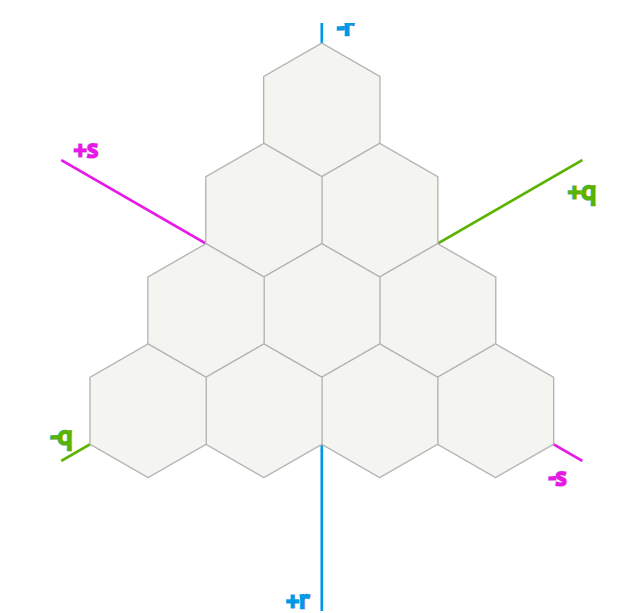
원래 본문을 읽을 때는 해당 Cube coordinate를 크게 이해하진 못했었다. 위 이미지도 바로 이해하지 못했었고 이러한 좌표계로 설정되있구나 하고 넘어갔었는데, 노트에 정육각형을 그리다가 정육면체를 위 이미지처럼 해당 각도에서 바로봤을 때 투영시키면 육각형이 나온다는 것을 알았다.

Cube coordinate를 이해하기 위해 별 생각 없이 3차원 좌표계에서 정육면체를 그리고 있었는데, 정육면체 육각형처럼 보이면서 이해가 되시 시작했었다.

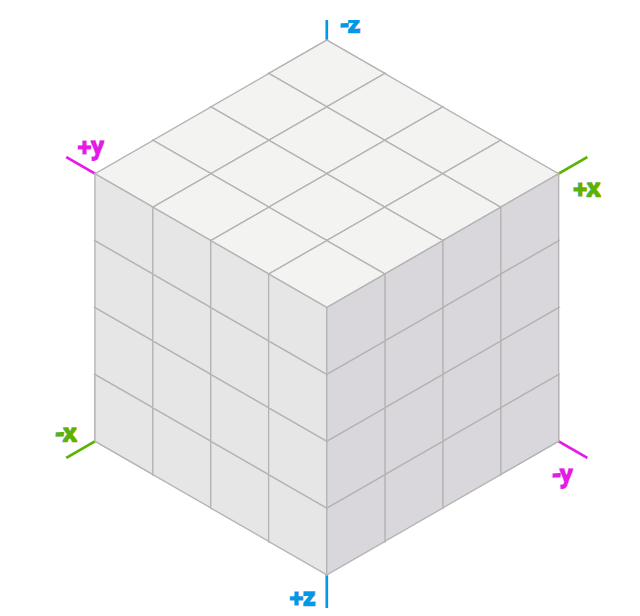
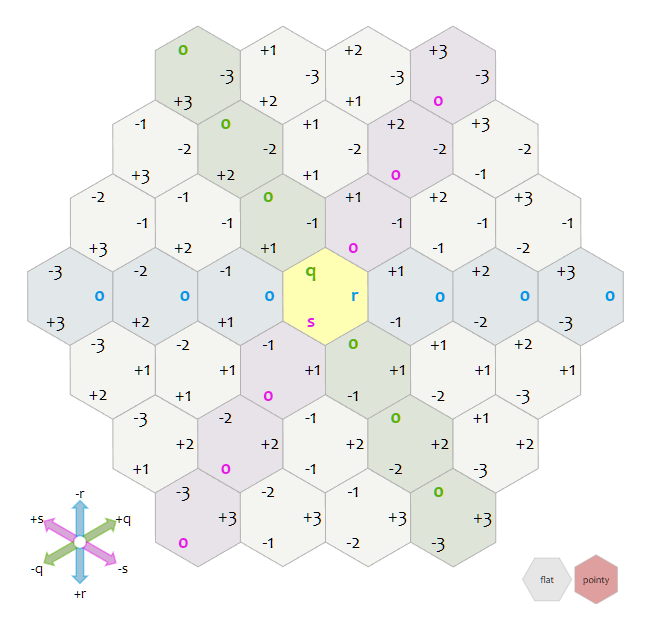
어찌 되었든, 이런 3차원 데카르트 좌표계의 특성을 이용할 수 있었기에 Offset 좌표계와 다르게, Cube, Axial 좌표계에서도 표준 벡터 연산인 덧셈, 뺄셈, 곱셈, 나누기를 모두 사용할 수 있으며 이는 알고리즘을 제작하는데 더 편하게 한다. 또한 3D 데카르트 좌표계에서는 distance, rotation, reflection, line drawing, 스크린 좌표로 변환과 같은 다양한 알고리즘도 있는데, 이 또한 육각형 그리드에서 작동할 수 있도록 조정하면 사용할 수 있다.
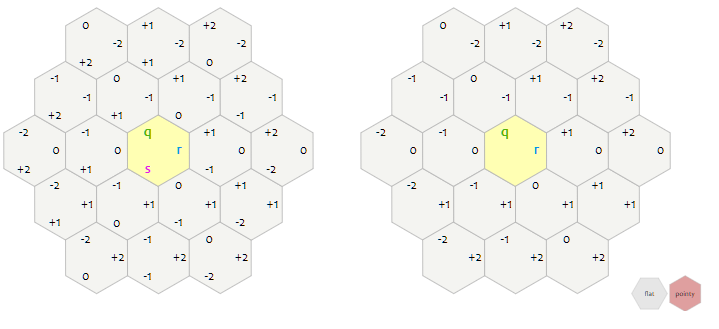
우측 Hex grid의 파란선, 초록선, 보라선은 각 q, r, s 좌표에 해당되는 좌표 값들이 고정되어 있는 것을 의미한다, 즉, 초록선은 q좌표가 동일하다는 의미이고 파란선은 r좌표가 동일, 보라선은 s좌표가 동일함을 뜻한다.
- q의 방향으로 움직일 때는 q, r 좌표가 같이 변하고 s의 좌표는 변하지 않는다.
- s방향으로 움직일 때는 s, r좌표가 같이 변하고 q좌표는 변하지 않는다.
- r좌표는 독립적이지 못하므로, r좌표에서 움직임이 발생할 경우, q또는 s좌표가 변한다.
이를 살펴보면, 육각형 그리드의 각 방향은 cube gird의 두 방향에 대한 조합인 것을 알 수 있다. 예를 들어, 육각형 그리드에서 북서쪽으로 이동한다면 s는 증가하고 r은 감소한다(`+s, -r`). 그래서 북서쪽으로 매번 이동할 때 마다 s에는 1이 추가되고, r에서는 1이 감소된다. 이 속성은 육각형에 근접한 neighbor을 구할 때 사용된다.
큐브 좌표계는 육각형 그리드 좌표 시스템을 위해 꽤나 합리적인 선택이다. 또한 $q + r + s = 0$ 제약 조건이 있어 알고리즘 연산을 수행할 때 이 조건을 만족시켜야 한다. 이 제약 조건은 각 육각형에 대한 표준 좌표가 있음을 보장한다.
$q+r+s = 0$ 제약조건이 있는 것은, 좌표계를 단순화 하기 위해 큐브 좌표계에서 $x + y + z = 0$인 평면만을 잘라내었는데, 이 성질이 똑같이 유지되는 것이다. 이를 통해 3차원 공간에서 2차원 공간으로 투영할 수 있게 된 것이다.
육각형 좌표의 움직임
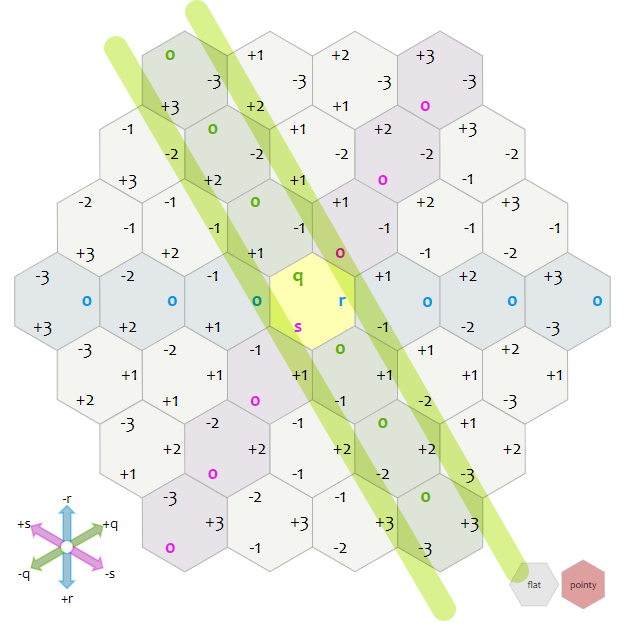
좌표의 움직임에 대한 하나의 팁이 있다면, 초록색으로 표시된 육각형은 q의 값이 고정인 상황이라고 하였다. 예를 들어 q의 값이 증가하는 방향이 헷갈린다면, 원점을 기준으로 q가 고정인 부분의 오른쪽영역은 증가하고 왼쪽인 부분은 감소한다.
Axial coordinates
Axial 좌표계는 trapezoidal, oblique, skewed 좌표계로도 불린다. Axial 좌표계는 s좌표를 저장하지 않는 점을 제외하고는 큐브 좌표계와 동일하다. $q + r + s = 0$ 제약 조건을 사용하여 필요시 $s = -q - r$을 통해 s좌표를 계산할 수 있기 때문이다. 이 또한 큐브 좌표계처럼 육각형 좌표에서 덧셈, 뺄셈, 곱하기, 나누기를 모두 지원한다. (offset 좌표는 지원하지 않음.)

이와 같은 사각형의 맵을 그리려면 Offset, Doubled 좌표계를 쓰는게 좋지만 이런 상황이 아니라면 그냥 Axial이나 Cube 좌표계를 사용하자.
Coordinate conversion
보통 axial이나 offset 좌표를 사용할 확률이 높지만, 많은 알고리즘을 간단하게 표현하기 위해서 axial, cube 좌표를 사용한 것들이 많다. 그러므로 필요시 양방향으로 축을 변환할 필요가 있다.
Axial Coordinates
축 좌표와 큐브 좌표는 본질적으로 동일하고, 큐브 좌표계는 s를 저장하지만 Axial 좌표계는 저장하지 않는다. 그러나 $s = -q -r$로 쉽게 구할 수 있음.
function cube_to_axial(cube):
var q = cube.q
var r = cube.r
return Hex(q, r)
function axial_to_cube(hex):
var q = hex.q
var r = hex.r
var s = -q-r
return Cube(q, r, s)사실 cube를 쓴다고 하면, r좌표만 무시하면 되서 axial좌표로 변환할 필요는 없고, axial 좌표를 쓰면 필요한 알고리즘에서 s만 계산하면 된다.
Hex to Pixel
이 내용을 이해하려면, 원문 아티클의 size와 spacing 다이어그램을 검토하는 것이 좋다.
Axial coordinates
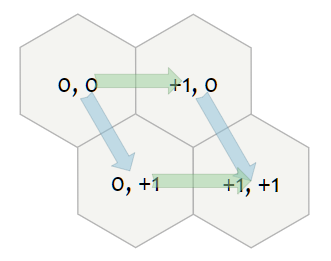
축 좌표의 경우, 육각형을 픽셀로 변환하는 것에 대해 생각해볼 수 있는 방식은 기저 벡터를 살펴보는 것이다. 화살표 (0,0) → (1,0)은 q의 기저 벡터($x=\sqrt{3}, \space y=0$)이고 (0,0) → (0,1)은 r의 기저 벡터 $ (x=\frac{\sqrt{3}}{2}, \space y=\frac{3}{2}) $이다. 픽셀 좌표는 `q_basis * q + r_basis * r`이다. 에를 들어, 육각형이 (1,1)에 있는 경우는 1개의 q벡터와 1개의 r벡터의 합이다. (3,2)의 육각형은 q벡터 3개와 r벡터 2개이다.
function pointy_hex_to_pixel(hex):
var x = size * (sqrt(3) * hex.q + sqrt(3)/2 * hex.r)
var y = size * (3./2 * hex.r)
return Point(x, y)이는 기저 벡터가 행렬의 열인 경우의 행렬 곱셈의 형태로도 볼 수 있다.

행렬 접근 방식은 나중에 픽셀 좌표를 다시 육각형 좌표로 변환할 때 유용하게 사용할 수 있다. hex-to-pixel을 pixel-to-hex로 다시 반전하려면 hex-to-pixel 행렬을 pixel-to-hex 행렬로 반전시키면 된다.
Neighbors
하나의 정육각형에 대해 인접한 6개의 정육각형을 구하는 것은 Cube좌표일 때 가장 간단하고, axial 좌표일 때도 간단한 편이다. 오프셋 좌표는 좀 까다롭고, 6개의 대각선 육각형을 계산해야 할 수도 있다.
Cube, Axial coordinates
정육면체좌표계에서 하나의 공간을 이동할 때 3 cube coordinate에서 하나를 +1로 변경하고, 다른 하나를 -1로 변경해야 한다(합은 0으로 유지 되어야 한다). Axial은 s좌표를 저장하지 않는 점 말고는 Cube와 동일하다

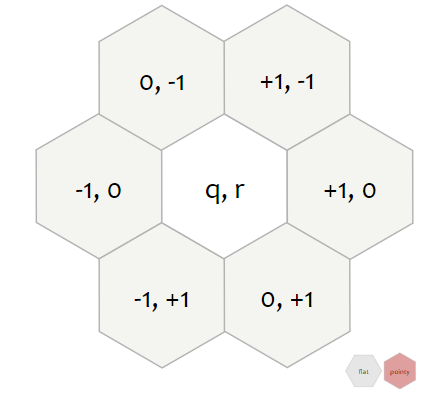
var cube_direction_vectors = [
Cube(+1, 0, -1), Cube(+1, -1, 0), Cube(0, -1, +1),
Cube(-1, 0, +1), Cube(-1, +1, 0), Cube(0, +1, -1),
]var axial_direction_vectors = [
Hex(+1, 0), Hex(+1, -1), Hex(0, -1),
Hex(-1, 0), Hex(-1, +1), Hex(0, +1),
]
위 처럼 방향 벡터를 설정해놓고 사용하면 편하게 사용할 수 있다.
Distance
Cube coordinate
Cube hexagonal 좌표는 3d cube 좌표를 기반으로 하기 때문에 거리 계산을 육각형 그리드에서 동작하도록 조정할 수 있다. 각 육각형은 3D 공간에서 큐브에 해당한다. 인접한 육각형은 육각형 grid에서 1만큼 떨어져 있어도 cube grid에서는 2만큼 떨어져 있다. 큐브 그리드에서 2step마다 육각형 그리드에서는 1step만 있으면 된다. 3D 큐브 그리드에서 맨해튼 거리는 `abs(dx) + abs(dy) + abs(dz)`이다. 이 거리가 육각형 그리드에서는 절반이고 코드로 보는 예시는 다음과 같다:
function cube_subtract(a, b):
return Cube(a.q - b.q, a.r - b.r, a.s - b.s)
function cube_distance(a, b):
var vec = cube_subtract(a, b)
return (abs(vec.q) + abs(vec.r) + abs(vec.s)) / 2
// or: (abs(a.q - b.q) + abs(a.r - b.r) + abs(a.s - b.s)) / 2
이를 작성할 때, 결과는 동일한 방식이 있는데 3개의 좌표중 하나가 다른 두 좌표의 합이어야 한다는 점에 주목한 다음 그 중 하나를 distance로 선택하는 것이다. 위의 2로 나누는 방식이나 최대값(max)를 사용하는 방식이나 결과는 동일하다.
function cube_subtract(a, b):
return Cube(a.q - b.q, a.r - b.r, a.s - b.s)
function cube_distance(a, b):
var vec = cube_subtract(a, b)
return max(abs(vec.q), abs(vec.r), abs(vec.s))
// or: max(abs(a.q - b.q), abs(a.r - b.r), abs(a.s - b.s))즉, 세 좌표 중 최대값이 거리이다.
절대값의 최대값이 거리인 이유
q, r, s 좌표는 각각 서로 다른 세 방향으로의 이동량을 나타낸다. 육각형 그리드에서는 이 세 방향의 이동을 통해 전체 이동 거리를 설명할 수 있다.
- 세 방향의 기여: 육각형 그리드에서 한 방향으로의 이동은 나머지 두 방향의 이동량에 비례한다. 예를 들어 (3, -5, 2) 벡터는 q방향으로 3만큼, r방향으로 -5만큼, s방향으로 2만큼 이동하는것을 나타낸다.
- 최대 이동량: 세 방향 중 가장 많이 이동한 방향이 전체 이동거리를 나타낸다. 이는 큐브 좌표의 특성상 한 방향으로 많이 이동할수록 다른 두 방향의 이동량이 줄어들기 때문이다. 예를 들어 벡터 (3, -5, 2)에서 r방향으로 -5만큼 이동했으므로 이는 가장 큰 이동량(절대값 5)를 나타내며, 전체 거리는 이 최대 이동량에 의해 결정된다.
- 거리의 정의: 큐브 좌표 시스템에서 거리는 한 방향으로의 이동량이 다른 두 방향의 이동량보다 클 때, 그 최대 이동량이 실제 이동 거리로 정의된다. 이는 육각형 그리드의 특성상 세 방향의 이동을 통해 전체 이동을 나타낼 수 있기 때문이다.
즉, 큐브 좌표 시스템에서 `q + r + s = 0`의 조건은 한 방향으로의 이동량이 다른 두 방향의 이동량을 상쇄시키는 것을 의미한다. 그래서 세 방향 중 가자 큰 절대값이 전체 이동 거리를 나타낸다.
여기서 좀 더 보충설명하자면 위의 설명을 (3, -5, 2)좌표를 기준으로 하였다. 그리고 우리가 가진 조건은 `q + r + s = 0`이라는 조건을 가지고 있다.
- r = -q -s도 가능하다.
- 결국 이는 r좌표로 이동하는 것이 q방향으로의 이동과 s방향으로의 이동이 합쳐졌다는 의미도 된다. 그래서, r방향으로 -5만큼 이동한다는 것은 q앙향으로 3만큼, s방향으로 2만큼 이동한 것과 같다. (각 축이 서로의 이동을 나누어 가진다.)
- 그래서 결국 큐브 좌표 시스템에서 하나의 좌표가 두 좌표의 이동을 포함하여 나타내기 때문에 세 좌표 중 절대값이 가장 큰 값이 실제 이동 거리를 잘 설명한다.
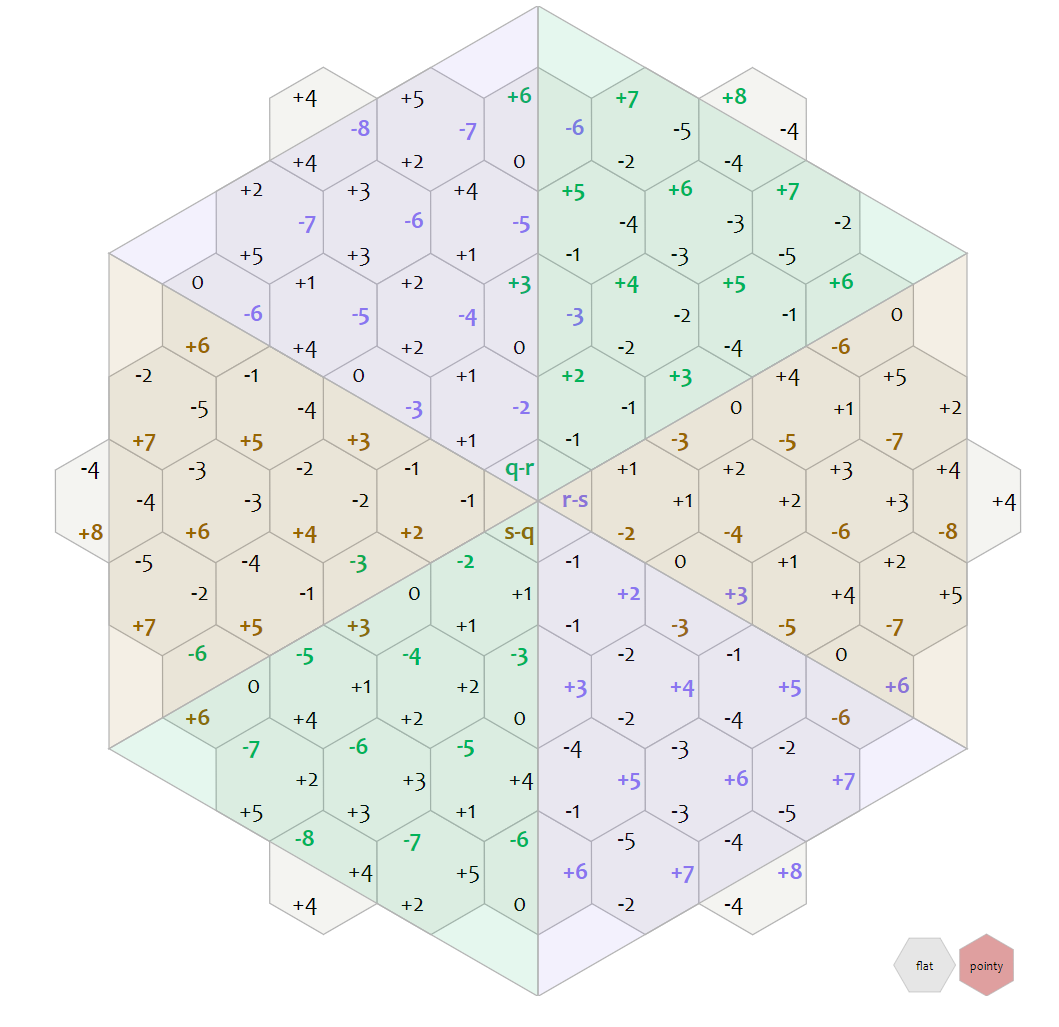
또한 `abs(vec.q-vec.r), abs(vec.r-vec.s), abs(vec.s-vec.q)`의 최대값을 활용하여 6개의 빗면 중 어떤 육각형에 속하는지도 알 수 있다.
Axial coordinates
Axial 시스템에서는 언제나 axial 좌표를 cube 좌표로 변경하여 거리를 계산할 수 있다.
function axial_to_cube(hex):
var q = hex.q
var r = hex.r
var s = -q-r
return Cube(q, r, s)
function cube_subtract(a, b):
return Cube(a.q - b.q, a.r - b.r, a.s - b.s)
function cube_distance(a, b):
var vec = cube_subtract(a, b)
return (abs(vec.q) + abs(vec.r) + abs(vec.s)) / 2
// or: (abs(a.q - b.q) + abs(a.r - b.r) + abs(a.s - b.s)) / 2
function axial_distance(a, b):
var ac = axial_to_cube(a)
var bc = axial_to_cube(b)
return cube_distance(ac, bc)위 코드와 같은 방식을 인라인 방식으로 표기하면 다음과 같다.
function axial_distance(a, b):
return (abs(a.q - b.q)
+ abs(a.q + a.r - b.q - b.r)
+ abs(a.r - b.r)) / 2$$a.s - b.s$$
$$ = -a.q - a.r - (-b.q - b.r) $$
$$ = -a.q - a.r + b.q +b.r $$
$$ = -(-a.q - a.r + b.q + b.r) $$
$$ = a.q + a.r - b.q - b.r $$
물론 다음과 같이도 쓸 수 있다.
function axial_subtract(a, b):
return Hex(a.q - b.q, a.r - b.r)
function axial_distance(a, b):
var vec = axial_subtract(a, b)
return (abs(vec.q)
+ abs(vec.q + vec.r)
+ abs(vec.r)) / 2
axial 좌표에서 육각형 거리를 쓰는 방법에는 여러 가지가 있다. 어떤 식으로 육각 좌표의 거리를 계산하든 axial 좌표에서 hex 거리는 맨해튼 거리에서 파생된다. 예를 들어 "difference of differences" 공식은 `a.q + a.r - b.q - b.r`을 `a.q - b.q + a.r - b.r`으로 작성하고, 2로 나누는 것 대신 최대값을 선별하는 max()를 사용한다. 큐브 좌표와의 연결을 확인하면 모두 동일 한 것을 볼 수 있다.
Movement Range
육각형의 중심과 범위 N이 주어졌을 때, 어느 육각형이 N step 안에 존재하는가?
육각형 거리 공식 `distance = max(abs(q), abs(r), abs(s))`에서 역으로 계산할 수 있다. N step 안에 존재하는 모든 육각형을 찾기 위해 ` distance = max(abs(q), abs(r), abs(s)) ≤ N`이 필요하다. 이 뜻은 세 가지 모두 참이어야 한다는 의미이다: `abs(q) ≤ N and abs(r) ≤ N and abs(s) ≤ N`. 절대값을 제거하면 `-N ≤ q ≤ +N and -N ≤ r ≤ +N and -N ≤ s ≤ +N`을 얻을 수 있다. 코드에서 중첩 반복문은 다음과 같다:
var results = []
for each -N ≤ q ≤ +N:
for each -N ≤ r ≤ +N:
for each -N ≤ s ≤ +N:
if q + r + s == 0:
results.append(cube_add(center, Cube(q, r, s)))위 루프는 동작하지만 다소 비효율적인 감이 있다. 반복하는 모든 s값 중 실제로 큐브 좌표에 대한 q + r + s = 0을 만족하는 값은 단 하나 뿐이다. 이 방법 대신 제악 조건을 만족하는 s의 값을 바로 계산한다:
var results = []
for each -N ≤ q ≤ +N:
for each max(-N, -q-N) ≤ r ≤ min(+N, -q+N):
var s = -q-r
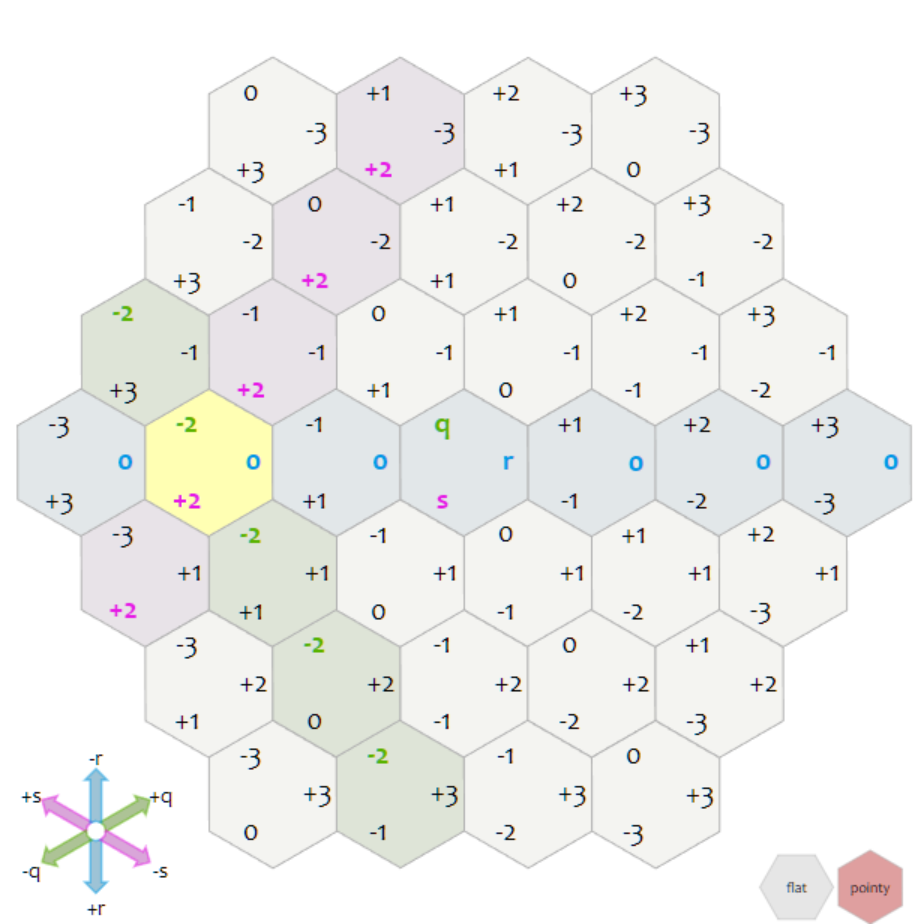
results.append(cube_add(center, Cube(q, r, s)))해당 루프는 정확히 필요한 좌표에 대해서만 반복한다. 다이어그램에서 각 범위는 한 쌍의 선으로 표시된다. 각 선은 부등신(반평면)이다. 6개의 부등식을 모두 만족하는 모든 육각형을 선택한다. 이 루프는 axial 좌표에서도 잘 동작한다.
var results = []
for each -N ≤ q ≤ +N:
for each max(-N, -q-N) ≤ r ≤ min(+N, -q+N):
results.append(axial_add(center, Hex(q, r)))
위 식을 사용할 수 있는 이유를 다시 세세히 정리해보았다.
$$ |q| \leq N, \quad |r| \leq N, \quad |s| \leq N $$
우선 반경 N에 있는 육각형들은 모두 위 부등식을 만족해야 한다. 여기서 $q+r+s=0$의 조건을 사용할 수 있는데, $q$나 $r$에 대해 부등식을 풀게 되면 s값이 식에 포함되게 되어 값을 구하기 어렵다. 그래서 $s=-q-r$을 사용하여 $q$와 $r$ 두 축을 활용하면 s값은 두 축에 의존하여 자연스럽게 구해지게 만들 수 있다. 이를 위해 $|s| \leq N$를 사용하며 다음 부등식으로 변환한다.
$$ |-q-r| \leq N $$
해당 식은 절대값으로 값이 감싸져 있는 특성을 활용하여 다음과 같이 부등식을 변형할 수 있다:
$$ -q-r \leq N, \quad -q-r \geq N $$
$$ r \geq -q+N, \quad r \leq -q-N $$
$$ -q-N \leq r \leq -q+N $$
위 부등식은 결국 $s=-q-r$에서 출발한 수식이기에, q값이 변함에 따라 r의 값의 범위가 조정되는 효과를 얻을 수 있다.
그렇지만 슈도 코드에서는 `max(-N, -q-N) ≤ r ≤ min(+N, -q+N)`을 사용하게 되는데, 이렇게 조건이 사용되는 다음 이유가 있다:
- `max()`의 의미는 가장 큰 하한을 구하겠다는 의미이다. $-q-N$만 사용하게 되었을 때는, q좌표가 점차 감소하게 될 때 범위의 한정이 없다. 그래서 N범위보다 작아지게 될 때는 $r$값을 $-N$으로 고정적으로 사용하게 된다.
- 또한 $-q-N$의 직관적 의미는 r의 탐색 범위가 넓어질 수록 q의 범위는 그만큼 좁아지는 경향이 있는데, 이 조건을 만족시켜준다. 예를 들어, r의 범위가 0~3이라면 q는 -3까지도 내려갈 수 있지만, r의 범위가 -1~3이 된다면 q는 -2까지 밖에 값을 가지지 못한다. 왜냐면 q와 r은 유동적으로 변하는 관계이며 총합이 $|N|$안에 있어야 한다. N자체가 3이라면, r의 최저값아 -1이라면 q의 최저값 -2까지만 사용해야 $|N|$범위 안에 있을 수 있다. (s값은 신경쓰지 않아도 되는 것이, q, r에 의존하여 자동으로 구해지는 것이다.)
- `Min()`은 가장 작은 상한을 구하겠다는 의미이다. 범위를 넘어가는 최대값을 제한하기 위해 $+N$을 사용하며 $-q+N$을 통해 반경 제약을 설정한다.
- $-q+N$의 직관적 이해 또한 q값이 커지게 될 수록, r에서 사용할 수 있는 값의 전체 범위는 작아지게 되는데, 이 제약 조건을 통해 반경 제약을 설정할 수 있게 된다.
어쨌든, Max와 Min은 r의 값을 지정해주기 위해 각 함수마다 조건 2개를 포함하고 있는 상태로도 볼 수 있다.

c++로 구현한 코드는 다음과 같다:
unordered_set<Hex> map;
for (int q = -N; q <= N; q++) {
int r1 = max(-N, -q - N);
int r2 = min( N, -q + N);
for (int r = r1; r <= r2; r++) {
map.insert(Hex(q, r, -q-r));
}
유니티에서 Hexagonal Grids
모든 연산은 Pointy Top 기준으로 수행되었습니다.
Rhombus 형태의 Hexgonal Grid 생성
void GenerateGrid()
{
// q와 r은 단순히 좌측의 하단부터 상단까지 차례대로 모두 순회할 수 있도록 설정된 변수. 실제 좌표는
// HexToWorldPosition() 함수에서 결정한다.
for (int q = -gridWidth; q <= gridWidth; q++)
{
for (int r = -gridHeight; r <= gridHeight; r++)
{
int s = -q - r;
CreateHex(q, r, s);
}
}
}
위 코드처럼 반복문을 순회할 때 아무런 조건도 지정해주지 않으면, q, r은 단순히 2차원 배열의 형태처럼 순회를 할 뿐이며,`CreateHex(int q, int r, int s)`에서 육각형이 설치될 World Position을 지정하게 된다.
Hexagon형태의 Grid 생성
void GenerateGrid()
{
// q와 r은 단순히 좌측의 하단부터 상단까지 차례대로 모두 순회할 수 있도록 설정된 변수. 실제 좌표는
// HexToWorldPosition() 함수에서 결정한다.
for (int q = -gridWidth; q <= gridWidth; q++)
{
for (int r = -gridHeight; r <= gridHeight; r++)
{
int s = -q - r;
if (Mathf.Abs(q) + Mathf.Abs(r) + Mathf.Abs(s) <= gridWidth)
{
CreateHex(q, r, s);
}
}
}
}
연산 속도 개선
void GenerateGridSecondVersion()
{
for (int q = -_gridWidthRange; q <= _gridWidthRange; q++)
{
int r1 = Math.Max(-_gridWidthRange, -q - _gridWidthRange);
int r2 = Math.Min(_gridWidthRange, -q + _gridWidthRange);
for (int r = r1; r <= r2; r++)
{
var (position, hexTile) = CreateHex(q, r);
if (CheckForPos)
{
Transform textObj = hexTile.transform.GetChild(0);
TextMeshPro textComp = textObj.GetComponent<TextMeshPro>();
// textComp.text = $"{q},{r}";
textComp.text = _count.ToString();
}
_count++;
}
}
}처음 짜여진 코드는 `(_gridWidthRange * 2) * (_gridHeightRange * 2)`만큼 순회를 하되, if문을 통해 필요한 부분만 남기는 형식이었다면 이 코드는 필요한 부분만 순회할 수 있도록 코드가 작성되었다. 해당 자료를 참조,


그러나, 아래 이미지 처럼 좌표가 입력되지 않아 이 따라 좌표가 생성될 수 있도록 수정이 필요하다.
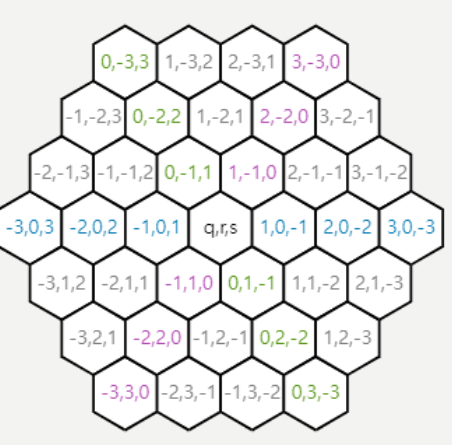
좌표 개선
Vector3 HexToWorldPosition(int q, int r)
{
float x = _hexSize * (Mathf.Sqrt(3) * q + Mathf.Sqrt(3) / 2 * r);
float z = -(_hexSize * (3.0f / 2 * r));
return new Vector3(x, 0, z);
}
원본 레퍼런스의 코드처럼 하면 좌표의 위치가 flip되서 나왔었다. 그래서 나는 z연산결과에 최종적으로 다시 $-$를 붙여 값을 반전시켜주니 제대로 나왔다. 나의 생각이긴 하지만, 아마 아래 이미지와 같은 Screen coordinate를 기준으로 연산을 했던 것이 아닐까 싶다. 이런 경우는 유니티의 world position의 방향과는 z축값이 반대로 형성되있기 때문이다. (여기서 나는 땅에 설치할 예정이기에 y에 대입할 값을 z축에 넣었었다.)

(사실 screen coordinate는 또 유니티 안에서는 (0,0)이 왼쪽 하단이라서.. 이런 용어 통일에 어려운 점이 존재하긴 한다.)
참고 자료
https://www.redblobgames.com/grids/hexagons/
https://www.redblobgames.com/grids/hexagons/implementation.html#shape-hexagon
'프로젝트 > HexaCraft' 카테고리의 다른 글
| [HexaCraft] Blender에서 Unity로 모델 임포트 (0) | 2024.09.10 |
|---|
