첫 번째 시도 방식 (X)
day를 기준으로 오름차순을 하고, 같은 날에선 가격을 기준으로 내림차순 하여 가능한 업무를 처리. 반례는 있다고 인지했지만, 다른 방식이 떠오르지 않아 먼저 해당 방식으로 구현해보았다.
#include <bits/stdc++.h>
using namespace std;
int n, p, d;
int dayCount = 1;
int ret;
vector<pair<int, int>> v;
bool cmp(pair<int, int> a, pair<int, int> b)
{
if (a.second < b.second) {
return true;
}
else if (a.second == b.second) {
// a.first가 더 크다면 true를 반환하며, b.first가 더 크다면 false를 반환. (이를 통해 조건문 2개 안써도 됨)
return a.first > b.first;
}
else {
return false;
}
}
int main()
{
cin >> n;
for (int i = 0; i < n; i++) {
cin >> p >> d;
v.push_back({ p, d });
}
sort(v.begin(), v.end(), cmp);
for (int i = 0; i < v.size(); i++) {
if (dayCount <= v[i].second) {
ret += v[i].first;
dayCount++;
}
}
cout << ret;
return 0;
}
두 번째 시도 방식 (O)
첫 번째 시도에서 존재했던 반례는 다음 예시로 보여줄 수 있다:
- (A) 강연료가 10, 기간이 1인 것
- (B) 강연료가 50, 기간이 2인 것
- (C) 강연료가 50, 기간이 2인 것
A,B,C 강연가 있을 때 A,B가 아닌 B,C를 선택하는 것이 이득이다. 즉, 강연 업무를 처리할 수 있는 기간 안에서 강연료가 가장 높은 강연들을 선택해야 한다는 명제를 설정할 수 있다.
이를 위해 p와 d를 한 쌍으로 가지고 있는 벡터를 d(강연 데드라인)를 기준으로 오름차순 정렬을 해준다. 날짜로 정렬을 하게 되면, 최소힙 구조의 우선순위 큐를 사용하여 해당 날짜 안에서 처리할 수 있는 강연료가 가장 큰 강연의를 선별 가능하다. 즉, 강연업무를 언제 할 것인지에 대한 배치를 고려하지 않아도 된다.
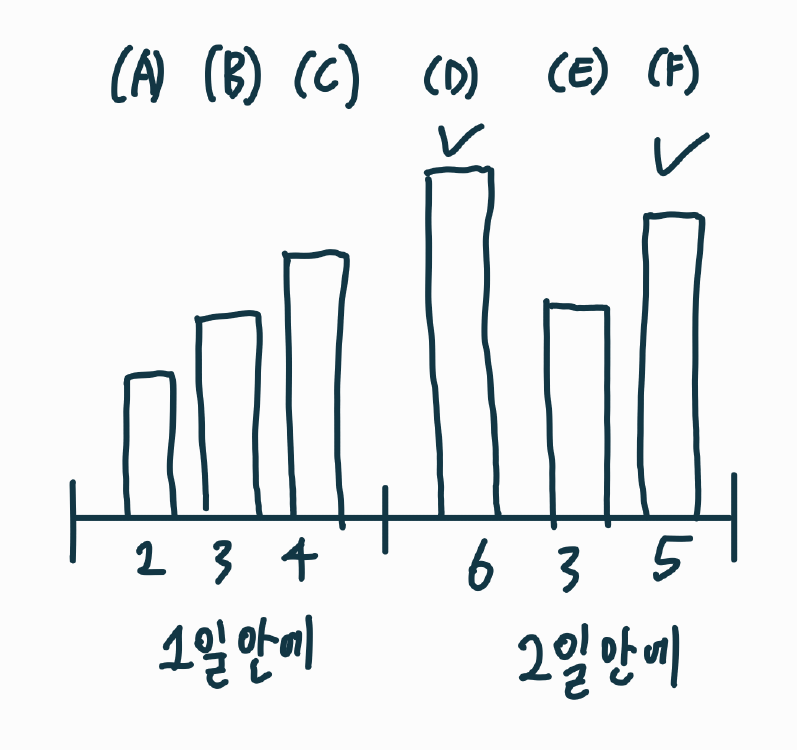
만약 위 그림과 같이 강연이 존재한다면, 2일 안에 처리해야 하는 D와 F를 선택하는 것이 가장 강연료를 높게 받을 수 있을 것이다.
또한 하루에 최대 하나의 강연만 할 수 있기 때문에, 우선 순위 큐의 크기는 강연 업무 데드라인의 크기를 넘지 않아야 한다. (7일 주어졌으면 최대 7개의 강연만 가능). 예를 들어, 1일 차에는 총 1개의 강연만 할 수 있으며, 2일 차에는 총 2개의 강연만 할 수 있기 때문이다. 이를 위해 날짜순으로 벡터를 정렬하여 강연을 정렬 한뒤, 강연료가 높은 강연을 선별하기 쉽도록 만든 것이다.
날짜순으로 벡터를 정렬했으니 처리할 수 있는 업무가 오름차순으로 증가할 수 있음을 예측 가능하다.
- 1일 안에 처리할 수 있는 가장 강연료 가 높은 것을 선택하여 다음 문제로 넘긴다.
- 1일, 2일안에 처리할 수 있는 가장 강연료 가 높은 것을 선택하여 다음 문제로 넘긴다.
- 1일, 2일, n일안에 처리할 수 있는 가장 강연료가 높은 것을 선택하여 다음 문제로 넘긴다.
해당 문제는 그리디 문제로, 최적 부분 구조로 전체 문제 최적 해를 구할 수 있어야 한다. 이를 통해 "강연 업무를 처리할 수 있는 기간 안에서 강연료가 가장 높은 강연들을 선택해야 한다는 명제"를 해결할 수 있게 된다.
아래 처럼 우선 순위 큐의 사이즈가 day(강연 업무 데드라인)를 넘겨버리면 pop()하여 강료가 가장 큰 값들만 남길 수 있다.

코드
#include <bits/stdc++.h>
using namespace std;
int n, a, b, ret;
vector<pair<int, int>> v;
priority_queue<int, vector<int>, greater<int>> pq;
int main()
{
cin >> n;
for (int i = 0; i < n; i++) {
cin >> a >> b;
v.push_back({ b, a });
}
sort(v.begin(), v.end());
for (int i = 0; i < n; i++) {
pq.push(v[i].second); // p 삽입
if (pq.size() > v[i].first) { // day보다 pq의 크기가 크다면
pq.pop(); // 최소값 pop
}
}
while (pq.size()) {
ret += pq.top(); pq.pop();
}
cout << ret;
return 0;
}
'역시 내 문제해결 알고리즘은 잘못됐다' 카테고리의 다른 글
| 백준 15829번 Hashing [C++] (0) | 2025.02.27 |
|---|---|
| 백준 9375번 패션왕 신해빈 [C++] (0) | 2024.10.22 |
| 백준 10989번 수 정렬하기3 [C/C++] (0) | 2021.02.21 |
| 백준 1978번 소수찾기 C/C++ (0) | 2021.01.10 |
| 백준 2908번 C/C++ (0) | 2021.01.03 |
