수학
[수학] Manhattan distance (맨해튼 거리)
Artiper
2024. 9. 21. 00:32
Manhattan distance
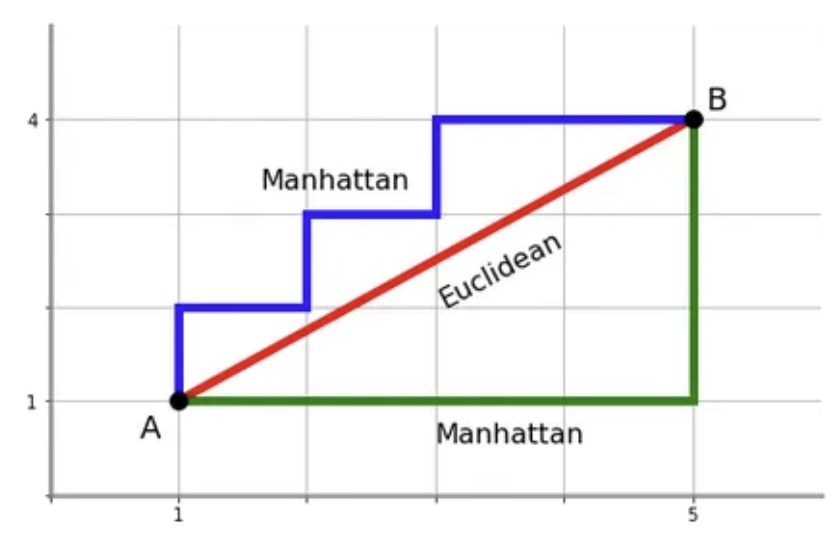
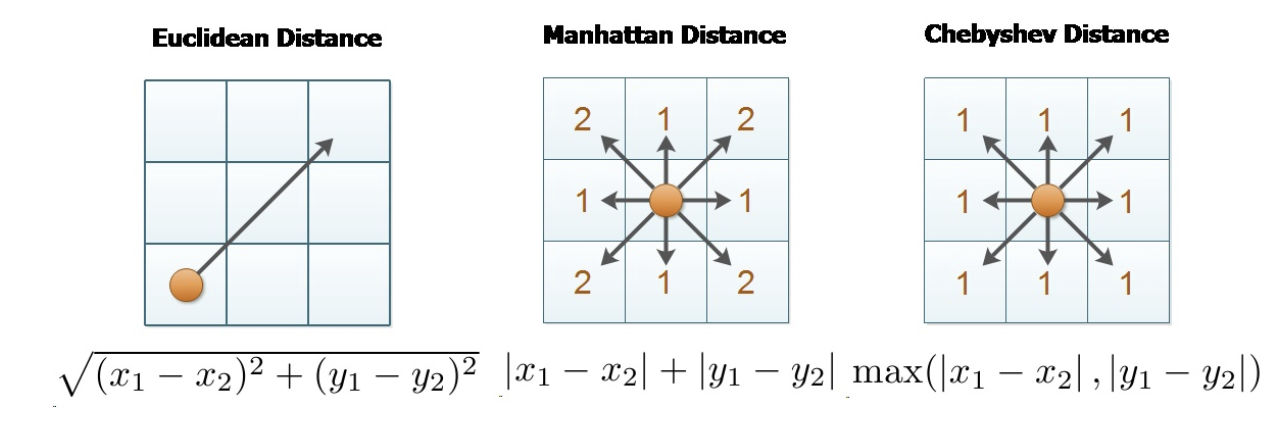
맨해튼 거리는 그냥 몇 칸을 이동했는지를 의미한다(선분 길의의 합). 유클리디안 거리는 시작점과 끝점이 주어지면 피타고라스 정리를 사용하여 구하게 된다. 맨하탄 거리는 몇 칸을 이동했는지를 보는 것이기에 x와 y각각 몇 칸 이동하였는지 계산하여 총합을 보며 다음의 식과 같다:
$$d_1(\mathbf{p}, \mathbf{q}) = \|\mathbf{p} - \mathbf{q}\|_1 = \sum_{i=1}^{n} |p_i - q_i|$$
- 맨해튼 거리: $d_1$
- 벡터: $p, q$
- $\mathbf{p} = (p_1, p_2, \dots, p_n)$과 $ \mathbf{q} = (q_1, q_2, \dots, q_n)$
머신러닝에서는 similarity 계산을 위해 사용했었는데, 지금은 어떤 Gird 내부에서 이동 거리를 위해 사용하고 있다.
참고자료
https://www.omnicalculator.com/math/manhattan-distance
https://iq.opengenus.org/euclidean-vs-manhattan-vs-chebyshev-distance/
https://ko.wikipedia.org/wiki/%EB%A7%A8%ED%95%B4%ED%8A%BC_%EA%B1%B0%EB%A6%AC